Kernel SVMs

Lets now apply the idea of a dual form representation to the SVM problem to have a kernel SVM. The dual representation helps us code the problem in the form of kernels and thus is very useful to solve for non-linear problem settings. Recall that in the original formulation of the SVM, the optimization problem is as follows: 
minimize 1/2|w|^2
subject to y_t(w'x + b) - 1 >= 0
This can be written in a dual form using Laggrangian and KKT conditions as follows: 
J(w, b; α) minimize 1/2|w|^2 - ∑(t=1:n) αt * (y_t(w'x + b) - 1) 
dJ/db = 0 =>  ∑(t=1:n) αt * y_t = 0
dJ/dw = 0 => w = ∑(t=1:n) αt * y_t * x_t = 0
Substituting it back, we get,
min ∑(i=1:n) αi - 1/2 ∑(i=1:n)∑(j=1:n)αi αj*y_i*y_j* xi'*xj  
subject to ∑(i=1:n)αi = 0
This optimization is still a quadratically constrained optimization and the matlab code for classification using the RBF kernel is shown as follows: 
%Generate Data
n = 50;
r1 = sqrt(rand(n,1)); % radius
t1 = 2*pi*rand(n,1);  % angle
d1 = [r1.*cos(t1) r1.*sin(t1)]; % points

r2 = sqrt(3*rand(n,1)+1); % radius
t2 = 2*pi*rand(n,1); % angle
d2 = [r2.*cos(t2), r2.*sin(t2)]; % points

x = [d1; d2];
y = [ones(n,1); -ones(n,1)];
n = 2*n;

%Construct RBF Kernel
K = zeros(n);
sig2 = 1;
for i = 1:n
    for j = i:n
        xi = x(i,:) - x(j,:);
        K(i,j) = exp( (-1/(2*sig2)) * (xi*xi') );
        K(j,i) = K(i,j);
    end
end

H = (y*y').*K;
f = -ones(n,1);
Aeq = y';
beq = 0;

%Run quadprog
qp_opts = optimset('LargeScale','Off','display','off');
[alpha, fval, exitflag, output, lambda] = ...
    quadprog(H,f,[],[],Aeq,beq, zeros(n,1), ...
    Inf*ones(n,1), ones(n,1), ...
    qp_opts);

% Find the support vectors
% calculate the parameters of the separating line from the support
% vectors.
svIndex = find(alpha > sqrt(eps));
sv = x(svIndex,:);
alphaHat = y(svIndex).*alpha(svIndex);

% Calculate the bias by applying the indicator function to the support
% vector with largest alpha.
[maxAlpha,maxPos] = max(alpha);
bias = y(maxPos) - sum(alphaHat.*K(svIndex,maxPos));

figure;
hold on;
plot(d1(:,1),d1(:,2),'r+')
plot(d2(:,1),d2(:,2),'b*')
plot(sv(:,1),sv(:,2),'ko');
axis equal

% plot decision boundary
[d1,d2] = meshgrid(-2:.1:2, -2:.1:2);
Xp = [reshape(d1,numel(d1),1) reshape(d2,numel(d2),1)];
m = length(Xp);
Z = zeros(m,1);

for i = 1:m
    xi = repmat(Xp(i,:),n,1) - x;
    xd = diag(xi * xi')';
    Kx = exp( (-1/(2*sig2)) * xd );
    Z(i) = Kx(svIndex) * alphaHat +bias; 
end
contour(d1,d2,reshape(Z,size(d1,1),size(d1,2)), [0 0] ,'k');
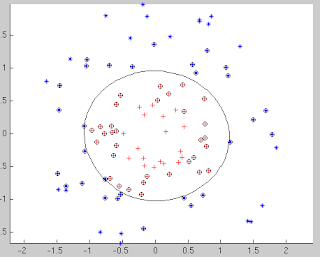
Finally, the figure showing the separation between the classes is as follows: The points that are circled are the support vectors. Note that a linear SVM would fail in such a case and using the kernel functions, we are able to get a beautiful separation in the data.

In this example, we used an RBF kernel which is infinite dimensional. Other popularly used kernels is the polynomial K(x,y) = (x.y +1)^p. The next question arises is what are the possible valid kernels ? A necessary and sufficient condition for a valid kernel is that the Gram matrix K should be positive semidefinite.

Comments

Post a Comment

Popular posts from this blog

MinHash, Bloom Filters and LSH

Lets talk about some large scale algorithms widely used in the document world. MinHash: Minhash is a really cute algorithm to determine how does a document compare to another. One simple way to compute document similarity is to compute the jaccard similarity between them. The jaccard similarity between the documents is computed as follows: def jaccard_similarity(set1: set, set2: set): if len(set1) == 0 or len(set2) == 0: return 0.0 common = len(set1.intersection(set2)) if common == 0: return 0.0 union = len(set1.union(set2)) return common / union One problem with Jaccard similarity is that it can take a lot of time to compute especially for large scale documents. The idea behind minhashing is to first operate on the space of document shingles. Shingles are basically any combination of k consecutive words of the document. For example, for the sentence "hi i am jaya" the possible 3 shingles are "hi i am" and "i am jaya&quo
Read more

Perceptron Algorithm

Image
The perceptron algorithm is a linear classifier using a linear function (w'x + b) to classify the points into two classes. The loss function for the perceptron algorithm just counts the points misclassified and then incrementally adjusts the weight vector and thus the decision boundary to appropriately classify the two classes. Perhaps this is the simplest algorithm one can think of to update the weight vector and is shown as follows: w(k+1) = w(k) + yt*xt if yt ≠ f(xt; w) i.e. we cycle through the training points and adjust the weight vector only if the points are misclassified. Note that our class labels are -1 and 1 and hence if the points are misclassified then y_t* f(xt; w) will be negative. In order to understand why the seemingly simple update rule works and leads to a convergence, lets closely examine it. One of the underlying assumption in the perceptron model is that the points are linearly separated hence there exists an w* such that y_t * f(xt; w*) ≥ γ for all t=1, 2
Read more

Logistic Regression

The logistic regression method even though called regression has a unique ability to give posterior probability values for a data point to belong to a particular class and hence serve as a discriminative function useful for classification. The idea is simple, to use the logistic sigmoid function on the linear function of feature vector. p(y = 1| x) = σ(w'x +b) The likelihood function can be written as p(t|w) = Π y_i^t_i*(1 - y_i)^(1 - t_i) ln p(t|w) = Σ t_i*ln(y_i) + (1 - t_i)*ln(1 - y_i) The error function is computed by taking the negative of the log likelihood function and is computed as follows: E(w) = -ln p(t|w) Now, ∇E(w) is computed as follows: y = 1 / (1 + exp(-w'x) Taking derivative of both sides, ∇y/∇w = exp(-w'x)(x)/(1 + exp(-w'x))^2 ∇y/∇w = xy(1-y) Substituting the value in ∇E(w), we get ∇ E(w) = Σ (y_i - t_i)*x_i The derivative of the error function is similar to the least squares problem, although we cannot obtain a closed form solution for it
Read more