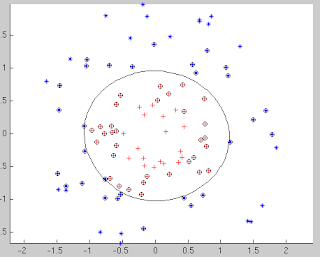
Logistic Regression
The logistic regression method even though called regression has a unique ability to give posterior probability values for a data point to belong to a particular class and hence serve as a discriminative function useful for classification. The idea is simple, to use the logistic sigmoid function on the linear function of feature vector. p(y = 1| x) = σ(w'x +b) The likelihood function can be written as p(t|w) = Π y_i^t_i*(1 - y_i)^(1 - t_i) ln p(t|w) = Σ t_i*ln(y_i) + (1 - t_i)*ln(1 - y_i) The error function is computed by taking the negative of the log likelihood function and is computed as follows: E(w) = -ln p(t|w) Now, ∇E(w) is computed as follows: y = 1 / (1 + exp(-w'x) Taking derivative of both sides, ∇y/∇w = exp(-w'x)(x)/(1 + exp(-w'x))^2 ∇y/∇w = xy(1-y) Substituting the value in ∇E(w), we get ∇ E(w) = Σ (y_i - t_i)*x_i The derivative of the error function is similar to the least squares problem, although w...